Autograd: 자동 미분¶
PyTorch의 모든 신경망의 중심에는 autograd 패키지가 있습니다.
먼저 이것을 가볍게 살펴본 뒤, 첫번째 신경망을 학습시켜보겠습니다.
autograd 패키지는 Tensor의 모든 연산에 대해 자동 미분을 제공합니다.
이는 실행-기반-정의(define-by-run) 프레임워크로, 이는 코드를 어떻게 작성하여 실행하느냐에
따라 역전파가 정의된다는 뜻이며, 역전파는 학습 과정의 매 단계마다 달라집니다.
좀 더 간단한 용어로 몇 가지 예를 보이겠습니다.
변수(Variable)¶
패키지의 중심에는 autograd.Variable 클래스가 있습니다. 이는 Tensor를
감싸고(wrap) 있으며, Tensor 기반으로 정의된 거의 대부분의 연산을 지원합니다.
계산이 완료된 후 .backward() 를 호출하여 모든 변화도(gradient)을 자동으로
계산할 수 있습니다.
.data 속성을 사용하여 tensor 자체(raw tensor)에 접근할 수 있으며,
이 변수와 관련된 변화도는 .grad 에 누적됩니다.
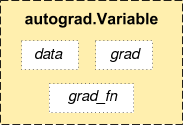
Variable
Autograd 구현에서 매우 중요한 클래스가 하나 더 있는데요, 바로 Function 클래스입니다.
Variable 과 Function 은 상호 연결되어 있으며,
모든 연산 과정을 부호화(encode)하여 순환하지 않은 그래프(acyclic graph)를 생성합니다.
각 변수는 .grad_fn 속성을 갖고 있는데, 이는 Variable 을 생성한 Function 을
참조하고 있습니다. (단, 사용자가 만든 Variable은 예외로, 이 때 grad_fn 은
None 입니다.)
도함수를 계산하기 위해서는, Variable 의 .backward() 를 호출하면 됩니다.
Variable 이 스칼라(scalar)인 경우(예. 하나의 요소만 갖는 등)에는, backward 에
인자를 정해줄 필요가 없습니다. 하지만 여러 개의 요소를 갖고 있을
때는 tensor의 모양을 gradient 의 인자로 지정할 필요가 있습니다.
import torch
from torch.autograd import Variable
변수를 생성합니다:
x = Variable(torch.ones(2, 2), requires_grad=True)
print(x)
Out:
Variable containing:
1 1
1 1
[torch.FloatTensor of size 2x2]
변수에 연산을 수행합니다:
y = x + 2
print(y)
Out:
Variable containing:
3 3
3 3
[torch.FloatTensor of size 2x2]
y 는 연산의 결과로 생성된 것이므로, grad_fn 을 갖습니다.
print(y.grad_fn)
Out:
<AddBackward0 object at 0x7fc227cd5cf8>
y에 다른 연산을 수행합니다:
z = y * y * 3
out = z.mean()
print(z, out)
Out:
Variable containing:
27 27
27 27
[torch.FloatTensor of size 2x2]
Variable containing:
27
[torch.FloatTensor of size 1]
변화도(Gradient)¶
이제 역전파(backprop)를 해보겠습니다.
out.backward() 는 out.backward(torch.Tensor([1.0])) 를 하는 것과 똑같습니다.
out.backward()
변화도 d(out)/dx를 출력합니다.
print(x.grad)
Out:
Variable containing:
4.5000 4.5000
4.5000 4.5000
[torch.FloatTensor of size 2x2]
4.5 로 이루어진 행렬이 보일 것입니다. out 을 변수 “\(o\)” 라고 하면,
다음과 같이 구할 수 있습니다.
\(o = \frac{1}{4}\sum_i z_i\),
\(z_i = 3(x_i+2)^2\) 이고 \(z_i\bigr\rvert_{x_i=1} = 27\) 입니다.
따라서,
\(\frac{\partial o}{\partial x_i} = \frac{3}{2}(x_i+2)\) 이므로,
\(\frac{\partial o}{\partial x_i}\bigr\rvert_{x_i=1} = \frac{9}{2} = 4.5\).
autograd로 많은 정신나간 일들(crazy things)도 할 수 있습니다!
x = torch.randn(3)
x = Variable(x, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y = y * 2
print(y)
Out:
Variable containing:
-1135.8146
785.2049
-1091.7501
[torch.FloatTensor of size 3]
gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)
print(x.grad)
Out:
Variable containing:
204.8000
2048.0000
0.2048
[torch.FloatTensor of size 3]
더 읽을거리:
Variable 과 Function 관련 문서는 http://pytorch.org/docs/autograd 에 있습니다.
Total running time of the script: ( 0 minutes 0.002 seconds)